Teorema de Modigliani-Miller
28-09-2023
Autores | Sin Impuestos | Con Impuestos
El teorema Modigliani-Miller (de Franco Modigliani, Merton Miller) es la base del pensamiento moderno en la estructura de capital. El teorema afirma que, en virtud de un mercado determinado (el paseo aleatorio clásico), en ausencia de impuestos, costes de quiebra e información asimétrica, esto es, en un mercado eficiente, el valor de una empresa no se ve afectada por la forma en que la empresa se financiada.
En ausencia de impuestos y costes de quiebra, no importa si el capital de la empresa se obtiene con la emisión de acciones o de deuda, ni importa cual es la política de dividendos de la empresa. Por lo tanto, el Teorema Modigliani-Miller es también a menudo llamado El Principio de irrelevancia de la estructura de capital.
Es la aparición de los impuestos corporativos y los costes de quiebra (riesgo de insolvencia), los que deshacen esa irrelevancia en la estructura de financiación ya que el coste de las deudas se reduce ya que es un gasto que se paga antes del impuesto sobre beneficios, pero solo hasta un determinado nivel, que es a partir del punto en que empiezan a crecer significativamente los riesgos de impago de las deudas(quiebra).
Este desarrollo teórico se plasta en un teorema que tuvo un planteamiento inicial sin considerar ambas variables: impuestos y riesgo de impago (insolvencia o quiebra), y que denominaremos Teorema SIN IMPUESTOS, y una segunda parte en el que veremos como afecta la inclusión de ambas variables y sus implucaciones al que denominaremos Teorema CON IMPUESTOS.
Autores del Teorema de Modigliani-Miller
Modigliani fue galardonado con el Premio Nobel de Economía en 1985 por esta y otras contribuciones.
Miller era un profesor de la Universidad de Chicago cuando fue galardonado con el Premio Nobel de Economía en 1990 , junto con Harry Markowitz y William Sharpe, por su trabajo en la "teoría de la economía financiera", con Miller citado específicamente por sus contribuciones fundamentales a la "teoría de las finanzas corporativas".
Teorema de Modigliani y Miller SIN IMPUESTOS
El teorema fue enunciado originalmente bajo el supuesto de la no existencia de impuestos corporativos (impuesto sobre beneficios). Se compone de dos proposiciones, que también puede extenderse a una situación de impuestos, como veremos posteriormente.
Consideremos dos empresas que son idénticos salvo por sus estructuras financieras. La primera (empresa U) no tiene deuda, es decir, que se financia con acciones solamente. La otra (empresa L) está apalancada: es financiada + en parte por acciones, y en parte por deuda. El teorema Modigliani-Miller afirma que el valor de las dos empresas es el mismo.
Proposición I:
Donde VU es el valor de una empresa sin apalancamiento = precio de compra de una empresa compuesta sólo de capital/acciones, y VL es el valor de una empresa apalancada = precio de compra de una empresa que está compuesta por alguna combinación de deuda y capital.
Para ver por qué esto debe ser cierto, supongamos que un inversionista está considerando comprar una de las dos empresas U o L. En lugar de comprar las acciones de la empresa apalancada L, podría comprar las acciones de U financiando la misma cantidad de dinero que la empresa L. La rentabilidad final a cualquiera de estas inversiones sería el mismo si el tipo de financiación del inversor es el mismo que el de VL. Por lo tanto el precio de L debe ser el mismo que el precio de U menos el valor de la deuda L.
Esta discusión también aclara el papel de algunos de los supuestos del teorema. El Teorema asume implícitamente que el costo de los inversores de pedir dinero prestado es la misma que la de la empresa, que no tiene por qué ser cierto (ante presencia de información asimétrica o en la ausencia de mercados eficientes).
Proposición II:
- ke es la tasa requerida de rendimiento por los acciones.
- k0 es el costo de capital medio ponderado o WACC.
- kd es la tasa de rendimiento requerida de los empréstitos, o el costo de la deuda.
- D/E es el ratio deuda-acciones (equity).
Un mayor ratio deuda/acciones conduce a un mayor rendimiento requerido sobre el capital propio (acciones). Debido al riesgo superior para los accionistas de una empresa con deuda. La fórmula se deriva de la fórmula del coste medio ponderado del capital (WACC).
Estas proposiciones son verdaderas asumiendo los siguientes supuestos:
- no existen los impuestos,
- no existen costos de transacción, y
- los individuos y las empresas pedir prestado a las mismas tarifas.
Estos resultados pueden parecer irrelevantes (después de todo, ninguna de las condiciones se cumple en el mundo real), pero el teorema todavía se enseña y estudia, porque dice algo muy importante. Es decir, la estructura de capital es importante precisamente porque una o varias de estas suposiciones es violada. Le dice dónde buscar los factores determinantes de la estructura óptima de capital y cómo esos factores podrían afectar a la estructura óptima.
Teorema de Modigliani y Miller CON IMPUESTOS
En este caso, la estructura de financiación si afecta al valor de la empresa. Esto se debe a que los intereses que se pagan por las deudas son un gasto a efectos del cálculo del impuesto sobre beneficios mientras que el dividendo (pago a accionistas) no es un gasto para el cálculo del impuesto ya que se reparten una vez pagados los impuestos.
Esto hace que a mayor endeudamiento el costo de capital medio se reduzca vía ahorros fiscales. Esta reducción del costo de capital aumentará el valor de la empresa porque reducirá el denominador de la ecuación de su valoración mediante el descuento de sus flujos de caja futuros donde la tasa de descuento será ese coste de capital
Proposición I:

El apalancamiento aumenta el valor de la empresa proporcionalmente a su endeudamiento.
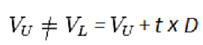
Proposición II:
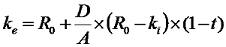
- ke es la tasa requerida de rendimiento sobre el capital propio o acciones.
- R0 es la rentabilidad que demandarían los accionistas si las deudas fueren 0. Esto es, si toda la empresa se financiase con Acciones.
- k0 es el costo de capital medio ponderado o WACC.
- ki o kd es la tasa de rendimiento requerida de los empréstitos, o el costo de la deuda.
- D/A es el ratio deuda-capital.
La rentabilidad demandada por los accionistas ke aumenta con el endeudamiento debido a la mayor asunción de riesgos, no así el costo de las deudas ki ya que al tener prioridad en el cobro sobre los accionistas, estan más protegidos y tienen más seguridad.
A continuación (siguiente) ampliamos la explicación de porque varía el valor de una empresa en base a su nivel de endeudamiento (distinta estructura de capital) y de donde parten esos ahorros fiscales (menores pagos de impuestos) mencionados. Finalmente veremos donde esta el límite al uso de las deudas como herramienta para aumentar el valor de la empresa (límite de los ahorros fiscales).

contacto | publicidad | legal | Política de Cookies | About EF
Enciclopedia Financiera, acercando la economía