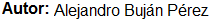Significatividad estadística
26-07-2018
La estadística rara vez da una respuesta simple de Sí / No a la pregunta en análisis. La interpretación a menudo se reduce al nivel de significatividad estadística aplicado a los números y se refiere a menudo a la probabilidad de un valor que rechaza con exactitud la hipótesis planteada.
El enfoque estándar es probar una hipótesis nula contra un hipótesis alternativa. La región crítica es el conjunto de valores del estimador que conduce a refutar la hipótesis nula. La probabilidad de error de tipo I es, por tanto, la probabilidad de que el estimador pertenezca a la región crítica dado que la hipótesis nula es verdadera (significación estadística) y la probabilidad de error de tipo II es la probabilidad de que el estimador no pertenezca a la región crítica dado que la hipótesis alternativa es verdadera. El poder estadístico de una prueba es la probabilidad de que rechace correctamente la hipótesis nula cuando la hipótesis nula es falsa.
Interpretación de los resultados
Hacer referencia a la significacitividad estadística no supone necesariamente necesariamente que el resultado global sea significativo en términos del mundo real. Por ejemplo, en un estudio amplio de un fármaco se puede demostrar que el fármaco tiene un efecto beneficioso estadísticamente significativo pero muy pequeño, de tal manera que el fármaco es poco probable que ayude al paciente notablemente.
Aunque en principio el nivel aceptable de significatividad estadística puede estar sujeto a debate, cuanto mayor sea el nivel significatividad estadística este permitirá rechazar la hipótesis nula con mayor contundencia. Esto es lógicamente equivalente a decir que la significatividad es inversa a la probabilidad de cometer un error.
Una diferencia pese a ser significativa estadísticamente puede ser de ninguna importancia práctica, pero es posible formular adecuadamente las pruebas para tener en cuenta esto. Una respuesta implica ir más allá de reportar sólo el nivel de significatividad. El valor de la significatividad, sin embargo, no indica el tamaño o la importancia del efecto observado y también puede parecer exagerar la importancia de las diferencias menores en estudios grandes.
Herramientas para comprobar la significatividad estadística
Un enfoque mejor y cada vez más común es informar los intervalos de confianza. Aunque éstos se producen a partir de los mismos cálculos que los de las pruebas de hipótesis, que describen tanto el tamaño del efecto como la incertidumbre que lo rodea.
Algunas pruebas y procedimientos estadísticos bien conocidos para confirmar la significatividad de las relaciones estadísticas son:

contacto | publicidad | legal | Política de Cookies | About EF
Enciclopedia Financiera, acercando la economía