Renta Temporal
01-01-2013
El siguiente paso en la matemáticas financieras, es calcular el valor de una renta. Con objeto de su estudio, distinguiremos dos tres casos por orden de complejidad de sus cálculos, de más complejo a menos complejo:
- Renta temporal en que las candidades o flujos NO tienen una relación de proporcionalidad (la renta de cada periodo es distinta al anterior y no siguen ningún patrón). Habituales en los flujos esperados del beneficio de una empresa,...
- Rentas temporales en que las cantidades o flujos SI tienen una relación de proporcionalidad (la renta de cada periodo es igual al anterior o sigue un patrón de crecimiento o decrecimiento). Habituales en los flujos esperados de deuda pública, bonos, depósitos, ...
- Rentas infinitas en que las cantidades o flujos SI tienen una relación de proporcionalidad (la renta de cada periodo es igual al anterior o sigue un patrón de crecimiento o decrecimiento). Habituales para la valoración inversiones sin vencimiento como acciones, rentas vitalícias, pensiones,...
El primer caso, el más genérico, corresponde, como ya hemos avanzado, a una renta de una duración determinada, en que las cantidades percibidas son distintas y sin relación entre ellas. Estas, nos permitirán explicar el concepto y posteriormente relacionarlas con los casos 2 y 3 que son casos específicos de este.
Antes de comenzar a analizar cada caso, si debemos precisar que, en estos casos, siempre utilizaremos el interés compuesto. También, debemos señalar que es especialmente importante para evitar errores, y antes de comenzar ningún cálculo, hacer la representación gráfica de los flujos, que consistirá en hacer una linea en la que indicaremos en que momento temporal se percibe cada cantidad. Esta herramienta nos permitirá asegurarnos cuantos periodos debemos descontar cada una de las cantidades.
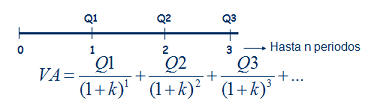
Siguiendo la imagen de la derecha, imaginemos una renta de las cantidades Q1, Q2, Q3,... que se cobran al final de cada periodo, 1, 2, 3,... El valor presente de esa renta temporal, consistirá simplemente en calcular el valor presente de cada una de las cantidades que componen la renta, tal y como representa la fórmula.
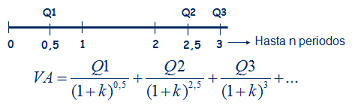
A partir de este sencillo ejemplo, podremos construir casos más complejos donde las cantidades tampoco sigan un patrón temporal, sino que se cobren en distintos momentos del tiempo, pero la base seguirá siendo la misma; el valor presente de las cantidades que componen la renta. Un ejemplo sería esta segunda imagen, donde los flujos no se producen al final de cada periodo, sino que se producen, Q1 a la mitad del primer periodo, Q2 entre el 2º y el 3º y Q3 al final del 3º. Además, se podría seguir complicando, considerando que el tipo de interés anual es distinto para cada cantidad, ya que no es lo mismo una operación aun año que a tres años (si por un depósito a 1 año pedimos un 5% anual, para un depósito a 3 años normalmente pediremos más de un 5% anual).
Como vemos, la parte más importante para el cálculo del valor de una renta, es comprender el momento temporal en que cada cantidad se produce, que es la base para conocer por cuanto tiempo deberemos retraerlo hasta el momento presente.
Fórmula renta temporal
Teniendo en cuenta el caso más genérico, podría expresarse como sigue:
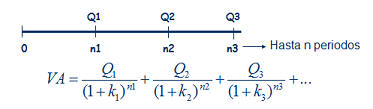
donde
VA.- Valor actual o presente de la renta considerada
Q1, Q2, Q3,... serían las cantidades que componen la renta
n1, n2, n3,... serían el momento temporal en que se recibe cada cantidad de
la renta
k1, k2, k3,... serían los tipos de interés para cada periodo
Además de los casos expuestos, donde hemos calculado el valor actual o presente, puede ser necesario el cálculo del valor futuro, como sería el caso del valor futuro de un plan de ahorro, por ejemplo, al que aportamos una cantidad mensual, trimestral o anual, que nos permitirá conocer que cantidad tendremos al final/vencimiento del producto. En este caso, en lugar de dividir cada flujo por el interés compuesto hasta el momento presente, únicamente deberemos multiplicar por ese interés compuesto hasta el momento futuro que deseemos.
A continuación trataremos las rentas temporales para el caso concreto en que estas sean constantes o con algún tipo de proporcionalidad entre ellas.

contacto | publicidad | legal | Política de Cookies | About EF
Enciclopedia Financiera, acercando la economía