Amortización de Préstamos
01-01-2013
El cuadro de amortización de un préstamo es la representación, en una tabla, de los distintos flujos financieros que lo componen: Principal, cuotas, y la descomposición de estas en la cantidad que supone devolución de principal y la parte que supone intereses.
Sistema Amortización Préstamo Francés
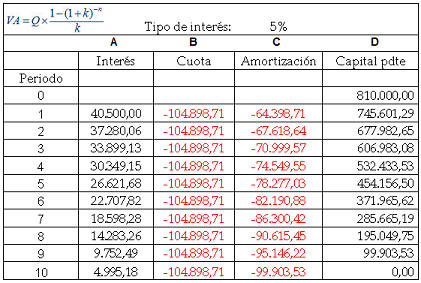
A la derecha, encontramos la tabla que representa la devolución d un préstamo con cuota constante (la cantidad que devolvemos periódicamente es siempre la misma) y que en el argot financiero se denomina sistema de amortización francés.
Como se puede apreciar, la Cuota es siempre la misma cantidad y para su cálculo se sigue la fórmula del valor actual de una renta temporal constante que se recoge en la parte superior izquierda. Así, VA sería el importe del préstamo, que en nuestro caso serían 810.000, Q sería la cuota (nuestra incógnita), k sería el tipo de interés que, en nuestro ejemplo es del 5% y n, el número de periodos, sería 10. Por tanto, sustituyendo en la fórmula obtendríamos que la cuota a pagar cada periodo del préstamo es de 104.898,71.
Una vez hemos resuelto nuestros cálculos, debemos elaborar la tabla que haríamos como sigue:
En primer lugar, incluiremos todos aquellos datos que conocemos. El capital del préstamo que son 810.000 en el momento 0 (momento en el que pedimos el préstamo y antes de haber devuelto nada) y que incluiremos en la casilla D0. Además, también conocemos la cuota de cada uno de los periodos del 1 al 10 que es de 104.898,71, cantidad que incluiremos en las casillas desde la C1 hasta la C10.
A partir de ahí, calcularemos el resto de casillas. ¿Cómo calcularemos los intereses?. Pues sencillamente, si la cantidad pendiente de devolver antes del periodo 1 (la del periodo 0) era de 810.000€ simplemente deberemos calcular el 5% de esa cantidad 40.500,00. Esta cantidad de 40.500,00 será los intereses del momento 1 que incluiremos en la casilla A1. Como la cuota del préstamo es del 104.898,71, el importe restante 64.398,71 irá dirigido a devolver el capital del préstamo, que se conoce con el término amortización del préstamo, e incluiremos en la casilla C1. Una vez que sabemos el capital que debíamos antes del pago de la cuota 810.000 y la cantidad de cuota que destinamos a devolver el principal 64.398,71, podremos calcular cuanto nos queda por pagar de capital pendiente que será la resta de ambas cantidades (D0-C1), esto es 745.601,29.
Sucesivamente seguiremos estos mismos pasos hasta llegar al momento 10 en el que, si los cálculos son correctos, el capital pendiente debe ser 0, ya que, con el pago de la última cuota, habremos devuelto la totalidad del préstamo.
Sistema Amortización Préstamo Alemán
En este caso, el sistema de amortización alemán o de amortización constante, en el que lo que es constante es la devolución del capital, los datos conocidos del cuadro de amortización serían tanto el capital inicial, como la Amortización de los 10 periodos que, al ser constante, sería de 81.000, y que incluiríamos en las casilla C1-C10. A partir de estos datos se calcularía el resto, teniendo en cuenta que la cuota B sería la suma de intereses + amortización (B1=A1+C1).
Sistema Amortización Préstamo Americano
Por último, en el sistema de de amortización americano, no se producen devoluciones de principal hasta el vencimiento por que lo la columna C sería toda 0 menos el periodo 10 en el que se devolvería la totalidad 810.000. Esto implicaría también que los intereses serían siempre los mismo 40.500 para los 10 periodos y las cuotas de los 9 primeros periodos también, hasta el décimo en el que se pagarían tanto el capital como los intereses de ese periodo 850.500.

contacto | publicidad | legal | Política de Cookies | About EF
Enciclopedia Financiera, acercando la economía